"Chapter. 0 - 함수의 연속"
게시글 주소: https://orbi.kr/00071303686
“Chapter. 0 – 함수의 연속”
안녕하세요 ‘한국외대 부’입니다. 언제나 여러분 입시에 가장 먼저 앞서있고,
길을 내주는 길잡이가 되어드리도록 최선을 다해 앞장서겠습니다!
오늘의 제목은 “함수의 연속”입니다. 모든 칼럼은 저의 자료의 내용으로 진행됩니다!
수2 내용의 함수 파트는 22번 15번 등으로 킬러로 자주 등장하는 내용입니다.
오늘은 킬러로 자주 등장하는 ‘함수의 연속’에 대해 알아봅시다.
함수의 연속은 함수를 결정하는데 중요한 조건이 됩니다.
수2에선 초월함수가 등장하지 않아 ‘연속’이라는 조건 만으로도 많은 정보를 알 수 있습니다!
특히, 수2에선 다항함수가 자주 출현하기에 연속과 미분 가능성에 대해서 항상 주의깊게 확인해야합니다.
연속임을 확인하는 방법은 정말 단순합니다.

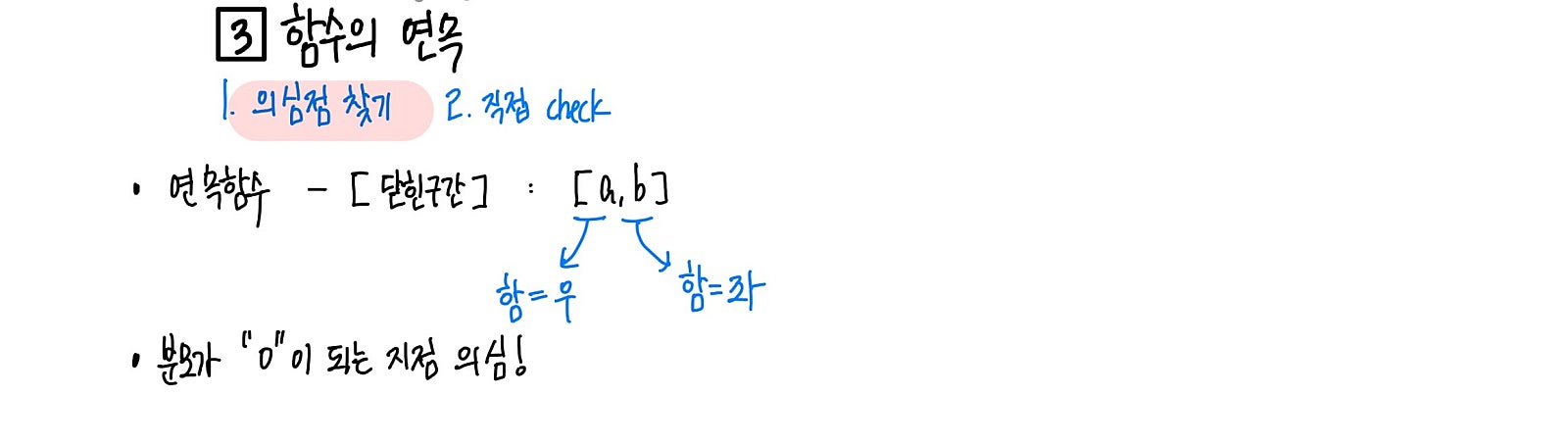
함수의 연속을 확인하는 의심점 찾는 방법을 확인해주세요.
먼저, 의심되는 지점에서 연속이 되는지만 확인하면 됩니다!
그 의심되는 지점을 어떻게 찾는지 알아봅시다.
첫 번째, 경계를 의심하자!
단순히 설명된 연속함수의 경우 닫힌 구간으로 정의된 그 경계가 의심점이 됩니다.
경계로 정의된 함수의 경우 경계 사이는 대부분 연속되는 구간으로 주어지고 그 경계에서 다른 함수로 바뀌거나 새로운 조건이 붙는 경우가 많습니다.
두 번째, 분모가 “0”이되는 지점을 의심하자!
분수로 표현된 유리함수의 경우 분모가 0인 지점을 항상 의심해야 합니다.
그 지점은 존재 자체를 안하기에 분모가 0이되는 좌,우 극한의 값과 같은 값을 지니는
다른 함수의 값으로 표현되어야 연속이 됩니다.
마지막으로, 합성함수의 연속에 대해 알아봅시다!

합성함수는 그 주인공이 무조건! 겉함수입니다.
그림과 함께 보면 합성함수는 두 개의 함수를 합성 시켜놓은 꼴이기에
두 개의 함수의 연속 의심지점을 모두 고려해야 합니다.
따라서 이와같이 속함수에서 겉함수로 넘어가는 부분을 꼼꼼히 체크해야합니다.
어느하나 빠지지 않게 잘 체크하여 그 좌,우극한 값과 함수값이 같은지 확인해야합니다.
합성함수의 연속을 잘 이해했나 확인해보기 위해
2016년 6월 모의고사 문제를 예시로 같이 풀어봅시다.


앞의 합성함수의 연속을 확인 하는 방법을 같이 보면서 해설을 읽어주세요!
속함수의 연속의 조건에서 경계인 x=1에서의 좌,우,함수값을 모두 의심해야하며,
그 값을 정의역으로 하는 g(x)에서의 값이 모두 동일해야하니
g(a)값은 g(1)의 값과 같아야 합니다, 따라서 이를 만족시키는 a의 모든 값의 곱은 1과 –1의곱인 –1입니다.
합성함수를 관찰할 때 중요하게 봐야하는 부분은
속함수의 치역이 겉함수의 정의역이 된다는 점입니다.
이점은 아직 미숙할지 몰라도 여러 예시 문항들을 풀어보면서 꾸준히 연습해야 합니다.
오늘의 내용은 여기까지 입니다!
앞으로 더 많은 내용들로 꾸준히 찾아올테니 좋아요과 구독 한번씩만 눌러주시고 기다려주세요!
자료의 전체버전은
https://cafe.naver.com/suhui/28704323 에서 확인해주세요!
고민이나 공부상담, 원하시는 칼럼의 내용이 있으시면 댓글이나 쪽지로 남겨주세요.
다음 칼럼에 반영하여 작성하겠습니다!
수험생의 길잡이가 되어드리는
'한국외대 부'였습니다 감사합니다!
0 XDK (+0)
유익한 글을 읽었다면 작성자에게 XDK를 선물하세요.
-

 좋아요 0 답글 달기 신고
좋아요 0 답글 달기 신고
-
얼버기 7
-
흠; 좆됏네
-
생윤은 칸트를 잘 가르치고 있다 - 수험생을 위한 칸트 정리편 2
*이 글은 필자의 뇌피셜이 난무하는 글입니다. 오늘은 교육 과정에서 멀리 뛰기...
-
아무도 없군 7
이제부터 여기는
-
궁금한거잇으신분 5
이래봐도 나름 6수 160 80 8의 스펙을 가지고잇음
-
주변에 여는가게가없네
-
상어 먹고 싶다 3
.
-
밸런스게임하자 27
밸런스게임 시켜줘 잘 답해볼게
-
서울대 3명보낸??평반~ㅈ반고이구... 모고 17 18번도 겨우풀수준이고 시험이...
-
굿나잇 2
ㄴㅇㅂㅈ
-
돈줘 2
돈내놔
-
너무졸리네 1
흠
-
인생 업적 1
구구단 외웟음
-
-
뻥임 안 보여줌 몇개 잇긴함
-
아이유 우울시계 이거 반복해서 들으면 눈물이 쏟아짐...
-
무물보 8
선넘질 ㄱㄴ
-
수능수학적 정보가 많은 칼럼보다 좀 경량급 칼럼이 호평받은거 나름 충격이라...
-
오목2 1
공격
-
오목 시작 0
가볼게요
-
자다가 깼네.... 안녕하세요? 처음 뵙겠습니다
-
ㄹㄹㄹㄹ 이러고 잇으면 머하나
-
사문 인강 1
임정환 듣다가 27강 도표에서 걸쳐서 무슨말을 하는지 도통알수없고 판서랑 책이랑...
-
현역 고3이고 이번 3모 화작 3개틀리고 74점 나와서 2떴는데 언매 해도...
-
새르비 1
새르비 여러분들 맞팔해요
-
새벽이라우울하군 1
잘까
-
연계였어서 그냥 쌩으로 물어봐도 될 문항을 빈칸형으로 15번에 박아서 물수학이란 평을 듣게함
-
다 나가네 걍 1
으음
-
5등급 현역 정파 국어 공부법 좀 알려줘 제발!!!! 간절함!!!!! 3
잉단 난 정신 개늦게 차림 고1 2학기때 정신 차린줄 알앗는데 아니엿고 고2때가...
-
수의대
-
더 푸는건 시간 좀 아까운데 그냥 자야겠다
-
D-221 0
영어단어 영단어장 day1 영어 어려웠던 문장 복습 힘 빼고, 휴식기간 가졌으니...
-
또 풀어볼까
-
의치한 중에서 어디든 괜찮은데 그래도 의대가 의료행위 할 수 있는 범위도 많고해서...
-
설수의 기원 3일차 12
설수의 오르비언과의 밥약도 기원.
-
그냥 순수하게 재미씀 읽고있으면
-
새벽엔 3
글 리젠이 안돼요 오르비 말고 할게 없는 옯붕이는 울어요
-
N티켓 괜찮네 4
쉬워보여서 안풀려다가 밤에 심심해서 푸는중 문제가 깔끔해서 재밌네
-
오이이아이오오이이이아이
-
못 막음
-
영상 봤음
-
이것만 올리고 자러갈게요
-
유지장치 4
교정기 유지장치 끼기 싫어서 일년을 안썼더니 원래대로 돌아왔어요 엄마 미안해 난 이대로 살게
-
이겨다
-
선착순한명 3
차단해드림 차단자리너무여유로움
-
고2 상위권 남학생, 생기부 너무 대충하는데 진짜 속터지네요. 내가 대학가냐 니가 대학가지…
-
슬슬 3
새르비 합류선언
-
아직도 적응 안 됨 나에게 미기는 미분기하학인데.. 심지어 비슷하기까지 하네 ㅋㅋ




































