[에라둔] 역학 문항에서의 미래와 과거
게시글 주소: https://app.orbi.kr/00069303116
계산적으로 중요한 내용들은 아니고 그냥 편히 읽으시면 될법한 내용들입니다.
역학 문항을 풀다 보면 여러가지 상황을 마주하게 되는데
종종 동일한 카테고리를 마주하게 됩니다.
이번에 다룰 내용은 어찌보면은 상대속도와 조금 관련이 있을 수 있습니다만 일단 접어두고.
아래 문항들의 공통점이 무엇일까요?
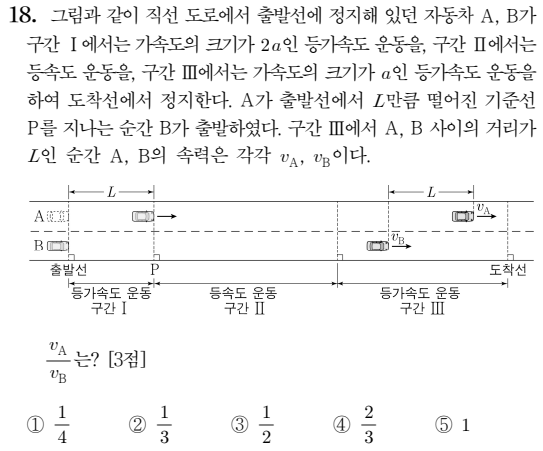

20230618


20210911


20130920
세 문항의 공통점은 두 물체가 모든 지점에 대하여 운동 방향, 속력 모든것이 동일한 상황들입니다.
이전에 저도 문항 출제를 할 때 위와 같은 상황을 이용하여 문항 출제롤 하곤 했는데
위와 같은 문항을 출제하면 참 좋은게 v-t그래프를 옆으로만 삭 밀어주면 되기 때문에
검토하기가 수월해서 즐겨냈었던 기억이 어렴풋이 납니다.
거두절미하고
어떻게 보면 위와 같은 문항들은 상대속도를 활용할만한 문항들 중에서도 특수한 케이스라고 생각을 하는데
저같은 경우에는 두 물체에 대하여 가상의 시간차 t를 가정하고 문제 풀이를 하는것을 선호합니다.
뿐만 아니라, 시간차 t가 난다고 생각하고 문항을 바라보면 좀더 문제 상황을 직관적으로 파악하기도 좋지요.


예를 들어 위 문항의 경우엔 B의 2초 뒤 모습이 A라고 생각하면서 풀면 문제 풀이가 아마 수월하겠죠.
일단 ㄱ이 바로 나올것이며
2초뒤 B가 정지할테니 평균속력 2라는 점에서 v=4가 바로 나올것이며
dv=4인동안의 시간이 2초니 가속도가 2인것도 술술 나올것입니다.


20210911
마찬가지로 위 문항도 B가 t초뒤의 A모습이라고 가정한다면 3vt=L이 나올것이며
우리는 자연스레 A가 p에서 q까지 이동하는데 걸리는 시간이 t라고 할것이기에
평균 속력 공식을 이용하여 1.5vt=0.5L과 같이 문항들이 순둥순둥하게 풀릴것입니다.
위와같이 동일한 경로, 운동 상황을 공유하는 문항의 경우에는 결국엔 대부분 문항에서 요구하는것은
두 상황에 대한 연립일것이며, 이 연립과정이 가감의 과정이기 떄문에
사실 t로 두고 문항을 풀면 쉽게 풀리는 경우가 많습니다.


20230618
위 문항의 경우에도 마찬가지로 역시 B의 t후 모습이 A라 생각하고 풀면 풀기가 수월할것입니다.
등가속도 운동 구간 I에서의 가속도를 2a라 하면 (0+2at)t/2=att=L이 나올것이며
이후 vb인 B가 시간 t 후 속력이 va가 된다고 하면 자연스레 (va+vb)/2 * t = L이 나오게 될것입니다.
그리고 구간 3에서 시간 t동안 속력이 변하였는데 이것이 va-vb일지 vb-va일지는 잘 모르겠습니다.
사실 시간 t라는 차이를 생각해보면 B가 출발할 때 이미 가속된 A가 있기에 거리차가 L보다 벌어질텐데
다시 L로 감소했다는 포인트를 보면 아마 가속도가 감소했음을 알기 수월하겠지요.
그러한 이유로 (va+vb)=2L/t, (vb-va)=at=L/t
va+vb : vb-va = 2:1, 2vb-2va = va+vb, 3va=vb, va:vb=1:3 이 나오게 될것입니다.
저같은 경우에는 두 물체가 동일한 경로를 운동하면 습관적으로 동일한 운동까지 하는지를 체크합니다.
아마 위와같은 유형들을 깔끔하게 푸시는 분들이라면 위의 개념을 숙지한 상태에서
그 이상은 본인의 직관, 암산 등으로 인한 최적화 정도의 차이만이 존재할것입니다.
만약, 위와 같은 수식적 풀이가 다소 어렵다면 그냥 모든 시간 영역을 t미지수로 두고 풀어보시거나
vt 그래프를 정성스럽게 그려보시는것을 권장드립니다.
아마 그래프를 그리시다 보면 자연스레 평행사변형과 친해지게 될겁니다.
0 XDK (+0)
유익한 글을 읽었다면 작성자에게 XDK를 선물하세요.
-
한완수 ㄱㅊ? 0
재종 들어가기전에 한완수 하려는데 괜찮음? 수학 3따리 턱걸이라 걍 노베임 교과개념부터 할까요?
-
댓글 너무 달려서 오르비 서버 터질까봐.
-
념글보내줘 5
갈거업ㄱ잖아딱히
-
ㅇㅈ 1
-
와 화력개빡세네 2
인증하면 세상사람들 다알겠다
-
다라 말했지만 니 래퍼 친구 내 flow 베껴가 나 의 해는 내 방안에 있지...
-
삼수망한후기 9
삶에대해다시생각하게됨 사소한것에감사하게된 게아니고그냥계속화남 억울함 사수하고싶음...
-
ㅇㅈ 14
펑
-
멍청한사람이싫어요 18
그래서내가싫어
-
ㅇㅈ 7
페페
-
수능 끝나고 코인은 +4천, 주식 -8천 빠진 것 같은데 수능 전에 이 꼬라지...
-
나때는 악뮤온다
-
여붕이라 안가도 됨 ㅇㅇ
-
2학년 모고 과탐을 지금까지 계속 화생으로 봤는데 수능때 도저히 화학 볼 자신이...
-
책 읽어야지 6
도 공공도서관에서 대여가 가능하더군요. 너무 비싸서 무료로 대여해 주는 공공도서관...
-
ㅇㅈ 9
아까 퇴근하면서 찍은거 ㅇㅈ 카메라 풀린거 너무좋고
-
총수라는 말은 11
야하다고생각해요
-
책 ㅁㅌㅊ 5
집에한가득w 시선으로부터는 사인도잇어요 알라딘에서냅다업어옴
-
원래 이시간에 먹는거올리면 최소 한 5~6개는 달려야되는데??? 다들 나 차단함??ㅠㅅㅜ
-
잠은 좀 이따 잘 듯 싶어요
-
선넘질받 12
부모유무는 물어보지마셈뇨
-
짜증나... 8
갈래
-
난 처음들어보는데 다들 아네..
-
책읽어요 3
재밌을거같아요
-
좋아하는책 몇개만 남겨두고 몇년 쌓인 책탑 싹다버렸는데 학교도 남초과의 그것도 일단...
-
나도 선넘질받 9
내일 논술 치는 기념으로
-
모썩철썩! 애응님이 그립네요 뭐 재르비해서 이 글 보고 있을 수도 있겠지만
-
아니 뭔가 별로 긁힐만한게 아닌 거 같은데 나도 모르게 묘하게 긁힘
-
남1여1해봣는데 둘다잘맞아서아직도실친으로지냄
-
ㄷㄷㅇㄷ 6
ㅓㅔㅠㅔ
-
진짜 고민됩니다 예비고3이고 가고싶은 대학이 정시로만 갈수있어 정시 준비중입니다....
-
그냥 찍는거? 아님 잘 맞춤?
-
20분 내에 개념 다 풀고 10분 내에 도표랑 도수분포표 풀기 도전!
-
지금 인사하면 받아줌? 24
-
씻고 옴
-
무려19시즌이엇다구 나보다오래햇다고??? 현생살아... 나도가끔오잔아
-
선넘질받 33
눈치보지말고 ㄱ 재미없으면 글삭할거임
-
탐구 안보고 국수영 반드시 세과목 모두 222 이내로 들어와야해요 수학 선택...
-
이제 지쳤다 0
그만~~
-
집 도착 9
-
장수생분들 계신가요 10
부끄럽지만 군대갔다온 02인데... 마지막으로 올해 수능봤고 마음같아선 예전부터...
-
다들착해요 방금전글보고 깜짝놀랐어요
-
인증메타 2
열린건가
-
직접 보진 못했지만 그렇게 전해들음
-
이미지 써드림 go 57
귀찮아지면드랍함
-
암기에는 도가 튼 표본과 강사진을 국경같은 지엽으로 변별하는 것은 이익이 크지 않음...
-
서울대식 400 0
어디정도 됨? +내 점수가 어디서는어메가는 399.5이고 텔그에서는 404.5인데...
-
아침에 글을 한번 썼지만 저는 지난 달에 로컬 회계법인으로 이직했고 올해 대거...
-
질답받아요 5
신체 주소 신상은 알아서 PASS하겠음
-
[사설]그냥 대학 장학금만 늘릴 게 아니라 졸업장 제값 하게 해야 0
교육부가 2025학년도부터 국가장학금 지급 대상을 중산층 자녀에게까지 대폭...












































옆동네 옆옆동네에서 잘 보고 있습니다감사합니다!!
와 쌤 과외 받았던 학생인데,,, 잘 계시나요 ㅠㅠ
감사했습니다!! 덕분에 카이스트 가서 잘 지내고있어요